En este tutorial vamos a crear un programa muy sencillo. Primero lo ejecutaremos en un simulador de ordenador cúantico y cuando lo tengamos terminado lo haremos en un ordenador cuántico de verdad (¡en serio!).
Para empezar necesitamos tener instalado python >= 3.5 y pip. Ahora instalamos qiskit.
1 | pip install qiskit |
Qiskit es un framework en python desarrollado por IBM que nos permite trabajar con ordenadores cuánticos, también podremos simularlos para los que justo ahora no tengáis un ordenador cuántico a mano. Empezamos!
Primero vamos a crear un circuito con dos bits y dos qubtis.
1 | import qiskit as qk |
Después de importar qiskit invocamos QuantumRegister, aquí le estamos pidiendo al framework que nos inicialice un array con 2 qubits. Los qubits son el equivalente cuántico a los bits de los ordenadores convencionales, tienen también dos posibles estados 0 ó 1, pero con algunas particularidades que vamos a ver más adelante.
A continuación, llamaremos a ClassicalRegister que nos crea un array con 2 bits convencionales donde iremos metiendo el resultado de los qubits.
Y por último, con QuantumCircuit crearemos un circuito virtual donde registramos nuestros bits y qubits.
Ahora vamos a leer el valor de nuestros qubits.
1 | qc.measure(qr[0],cr[0]) |
Aquí estamos pidiendo al circuito qc que lea el valor de los qubits en qr y meta el resultado en sus respectivos bits en cr.
Por último, instanciaremos el simulador para hacer las pruebas y le pediremos que ejecute el circuito qc 1000 veces.
1 | backend = qk.BasicAer.get_backend('qasm_simulator') |
Si ejecutamos el código veremos lo siguiente.
1 | {'00': 1000} |
Esto quiere decir que la consulta del valor de los 2 qubits durante las 1000 ejecuciones simpre ha sido 0.
Superposición
Como veis, nuestro programa cuántico no hace nada muy cuántico pero ahora empieza lo divertido.
Añadimos la siguiente línea a nuestro código justo antes del primer measure.
1 | qc.h(qr[0]) |
Con esta simple línea estamos diciendo al circuito qc que añada una puerta lógica cuántica al qubit que hay en la posición 0 de nuestro array de qubits (qr). Es decir, qc.h es un equivalente cuántico a los AND, OR, XOR etc y con él estamos añadiendo al qubit la puerta de Hadamard.
La puerta de Hadamard nos permite añadir superposición a nuestro qubit. Simplificando mucho, esto quiere decir que nuestro qubit entre medición y medición va a estar entre 0 y 1 al mismo tiempo aunque sea poco intuitivo.
Si nos imaginamos una esfera donde el polo superior es 0 y el inferior es 1 la superposición son todos los otros puntos posibles en la superficie. En resumen, un bit puede contener un valor (0 ó 1) pero un qubit contiene ambos valores (0 y 1).
 https://es.wikipedia.org/wiki/C%C3%BAbit#/media/File:Bloch_sphere.svg
https://es.wikipedia.org/wiki/C%C3%BAbit#/media/File:Bloch_sphere.svg
Pero cuando medimos nuestro qubit le “obligamos” a decantarse por 0 o por 1.
Si volvemos a ejecutar el código veremos algo así.
1 | {'00': 508, '01': 492} |
En este ejemplo el qubit que hemos puesto en superposición ha sido “1” 492 veces de las 1000 que lo hemos medido, el otro qubit que todavía no hemos tocado es 0 siempre.
Entrelazamiento
Ahora vamos a desencadenar un entrelazamiento que es incluso más raro que la superposición. Cuando entrelazamos 2 qubits estos se influencian independientemente de la distancia a la que se encuentren. Es como si la información se teletransportase…
Para enlazar nuestros dos qubits añadimos esta línea a continuación de la superposición.
1 | qc.cx(qr[0], qr[1]) |
Aquí estamos añadiendo la puerta CNOT que se encarga de entrelazar nuestros dos qubits, esto quiere decir que cuando midamos qr[0] automáticamente qr[1] se volteará solo si qr[0] es 1.
Si ejecutamos el código obtendremos el siguiente resultado.
1 | {'00': 496, '11': 504} |
Cuando los medimos qr[0] y qr[1] siempre dan el mismo resultado .
Circuito
Este es el estado final de nuestro circuito que podéis ver con print(qc.draw()).
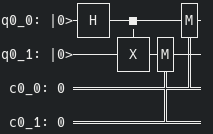
q0_0 y q0_1 son los dos qubits, con la H podemos ver donde hemos aplicado la puerta de Hadamard, con la X vemos que q0_1 está entrelazado con q0_0 y, por último, M son las mediciones de los qubits que guardan valores en los bits c0_0 y c0_1.
Ordenador cuántico real
Ahora que hemos terminado vamos a quitar el simulador y ejecutar el código en un ordenador cuántico real.
Para ello podemos usar uno de los 4 ordenadores cuánticos entre 5 y 16 qubits que IBM ofrece gratuitamente.
Para hacerlo tenemos que registrarnos en IBM Q y generar un token aquí.
Modifiquemos el código. Primero vamos a poner el token que hemos generado y nos autenticamos.
1 | token = "TOKEN" |
Segundo vamos a usar qiskit para que nos diga el ordenador cuántico menos ocupado para ponernos en la cola de ejecución. Como nuestra app solo necesita 2 qubits nos vale cualquiera.
1 | from qiskit.providers.ibmq import least_busy |
Y lanzamos nuestro script. Esta vez la respuesta no será inmediata depende de lo ocupado que esté el ordenador.
1 | {'11': 345, '10': 102, '00': 489, '01': 64} |
Como podéis ver, mi resultado es diferente al simulador. Tenemos una minoría de ‘10’ y ‘01’ eso significa que el entrelazamiento no ha funcionado como se esperaba, esto es normal, estamos usando prototipos de ordenadores cuánticos y todavía no son perfectos.
Esto es todo. ¡Enhorabuena!. Has ejecutado tus primeras líneas de código en un ordenador cuántico real.
